Sree Iyer: Good morning, welcome to episode number 64 of daily Global insights, Namaskar Sridhar Chityalaji, it is the 30th of December. Welcome to PGurus Channel. And today we are going to hit the ground running. There’s a lot of stuff to cover. I’m sure you are all eager to know what has been happening with the stimulus bill and as well as the Gallup poll findings that Trump is the most popular person. There’s a lot of data behind that we’re going to share. This is a very objective look at why he’s got that and before we proceed, please do watch this program in its entirety. And also if you like our Channel, please do click the like button and if you have not subscribed, please subscribe. Sridharji Namaskar and welcome to PGurus Channel.
Sridhar Chityala: Namaskar and good morning to all on you know one day, sorry two days prior to the end of 2020. Everybody would like to see the end of 2020 and move on to 2021. So, good morning and looking forward to the next half an hour or so.
Sree Iyer: Sir, let’s start with what happened yesterday all that drama about Mitch McConnell, first, he turns down The House offer and then after a few minutes or a few hours, there’s a rethink and then he submits it slightly better Kinder gentler version. But, if you look at some of the media reporting, it almost looks like this new proposal of which Mitch McConnell it’s sort of like a guaranteed to fail for the $2,000 per person effort. What are your thoughts on it, sir?
Sridhar Chityala: Well, I think that is a political drama that is being played out. It’s like when you have these moments of opportunity, that’s when you exert your influence and pressure. Otherwise, you are a great good citizen in obedient and compliant with rules of engagement. So, the house everybody wakes up and says we got to pass the 2,000 dollars bill. The two Senate candidates contesting the Georgia election say we got to pass it because the President is saying it, the people are saying it, and really the economy needs it because the covid has taken a bit longer so everybody is saying it. So, Mr. McConnell says no, no, you all can pass the Bill, we’re not going to support the Bill.
So, the house passes the bill, but then it had a couple of riders stuck on it and then those riders got eliminated in some way which is the article 230 to be either eliminated or watered down significantly. And then lo and behold Nancy Pelosi concedes ground for conducting a hearing on the election fraud. So, then GOP Senators quite a few of them line up and say yeah, we got to support this bill, we got to support them, so, some more and more Republican Senators come online and still, Mitch McConnell says no. And then around 7:30 p.m. New York Times, East Coast time, we get the flashing press release Mitch McConnell says the 2,000 dollar bill stimulus will be approved. I’m standing by it, it will be presented for a voted for an up or down vote in the Senate. We are willing to forego article 230. We will also consider and look at the defence bill and we are prepared to hold the hearings on the election finding. So, therefore and we also will look at the wasteful expenditure. So, all Presidents’ conditions, which was the rationale for the veto is now accepted by Mr Mitch McConnell. So, what then happens if let’s say Mitch gets his votes in the Senate, do they go back? Because, if they say article 230 is gone. Okay, Nancy may say good that’s gone. 2,000 dollars is accepted, that’s good, so that’s done. And by the way, you know, there will be election stuff. Okay, that’s good. Then, he says I’m going to pull this pork bellies down. So, then what happens, that’s the question that remains uppermost. I do not believe that they will say okay, let it go and we’ll figure this and fight this on another day. Now, nobody wants to accept it because the reason is everybody here is a President Trump hater by and large. But, the survey doesn’t say so, at least when you listen to the media here, you hear the story that everybody hates President. So, President ineffectively has got his way $2,000, he got it increased, that’s number one. Number two, he put wasteful expenditure, the wasteful expenditure will be watered down. He got Article 230, he got, therefore, the defence bill as well through with the Article 230 condition being met. And he basically went on to say it’s not $600, it’s $2,000 and more is coming to address the small business. So, it’s a very fascinating way as to how a president has played a very proactive role in managing the House and Senate and bringing it almost close to what he had proposed as his terms. As I said, the US media and generally around the world, they won’t accept because, they have bit visceral hatred for President Trump, but he has achieved the goal.
Sree Iyer: Well, did the Gallup poll finding have something to do with Mitch McConnell’s change of mind, let’s find out. So what we thought viewers? We would do, was let us try and objectively analyze the last four years of trump and compare it with his predecessor Barack Obama and see how the two fared although it is unfair because Trump got only four years, whereas Barack Obama got eight years, but that’s okay. We are going to give him a little bit of handicap. What’s SridharJi and I have done, is put together an objective view as to how Trump’s candidacy has changed the lives of average Americans and perhaps, the whole world also, because if you remember it Trump was instrumental in having many West Asian countries.
Sir, I am using the word West Asia, West Asian countries normalized relations with Israel, and this is something that nobody has done before also Trump kept America out of any new Wars. So, these are some of the highlights of nobody can deny that as it may, now let us plunge right into an objective analysis of why Trump got the most popular status or the vote for most popular.
Sridhar Chityala: While you bring up the screen sir, so I’ll say here, the three key headlines, Gallup poll says that President Trump has been voted the most popular American of the year for 2020, with 18% of the respondents until last year he tied with President Obama, I think about 16% or so. This year, this is the Americans voting for past presidents and important leaders and so on I think, you will probably see a chart which shows, what percentage? Of course, I don’t see, I’m looking at Sree IyerJi, you probably are looking at the screen, So I think that you will probably see that. The second important thing is that they conducted a poll among the Republicans, 72% of the Republican voters basically said that Trump should be the role model for GOP the way he has transformed the party and that simply implies that he has broadened the masses and once upon a time Republican party was at least construed as a specific white denomination only for affluent business people, it was a private Social Club, etc. Etc. He has completely defied that specific logic and so in other words, so you find that the 72% of the Republican voters saying that he is the right role model, especially around what he has done in 2020. The results also suggest there is very strong support for President Trump to continue even today, notwithstanding the fact that he is almost reached the end up his term, it’s almost December 31st. So, there’s probably a strong indication that also gives a pep up which is to say contest contest contest because the elections, there is a lot of questions around the elections in terms of the validity and the transparency of the elections. 56% of the Americans that’s Democrats, Republicans, Blacks, Whites, Hispanics everybody you can think of has voted that their life is much better in 2020 relative to where they were in 2016 and he stands tall amongst that relative to any of the incumbents before that is 1990, 1984, 1992 to 2004 and 2012. So, now, we’ll get to the charts as to what has led to this magical outcome that Trump has been able to accomplish.
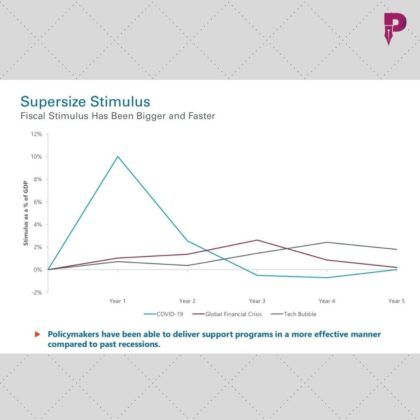
Sree Iyer: So, I have the first chart put up the super-sized stimulus that had to be passed to tie the country and in fact the world over on the covid crisis. So I have the first chart up on the super-sized stimulus are go ahead.
Sridhar Chityala: Yeah great. So I think as Sree IyerJi pointed out, this is the first parameter, what is the significant criteria that differentiate? You will see that there are three graphs one is October covid-19, the second one is the global financial crisis, which is one of Mr Obama took over and then there was the tech bubble. When you compare these three charts, you will see a huge spike in year one which is equal to 10%, the star chart was constructed in September. We will construct another chart in January, once the second stimulus comes in 10% of the GDP. And then yes, you can see it tapers down as you move towards Year five is just smoothening, which is purely based on the forecast of the GDP numbers and which is to say effectively in year two, once we cast crossed year two from almost from year 3 onwards, we are below the zero lines, which is effectively the fiscal stimulus will be taken out. That is reflective of the second stimulus that was induced right now and whether that kicks in the last two days or whether that kicks in the first quarter of January of the thing, we will factor in but that kicker that happened as opposed to the other two stimuluses, you can see they have tapered over the three years. In our view that basically has delayed the momentum of the recovery and so, this is a very key differentiator where a strategic decision was taken in terms of putting a significant amount of stimulus into the economy. Now, it is not just simply putting the stimulus, now we go to the next chart, they were targeted and directed across the various sectors of the economy.
Sree Iyer: It’s absurd
Sridhar Chityala: it’s up. So, you will find that you have direct payment to people that’s number one. Two, you have a PPP program that was introduced to ignite the small business, which is the chunk of the industry that we are people are employed. Then, the third they did not leave the corporate sector, they put money into the corporate sector as well close to 500 billion dollars was put into the corporate sector. I’m just looking at it because I don’t have the benefit of your chart, so I’m taking a look to make sure my numbers are correct. Then, they put 377 billion dollars need to the small business sector. The government also employs a significant amount of people they put 17% into government and they put 9% into public services. So, the sectors which are consumptive but which are also employers of the economy, they directed the stimulus and applied it so that the impact can be directly felt.
Three questions are asked in hindsight today in 2020 at the end of when we were in November December. Three questions are asked, why is this economy looking so well relative to a pandemic type of a situation, when we have between three to six months of shut down people remote working from home? The next chart which is the retail sales chart will give you that number.
Sree Iyer: I have it up, Sir.
Sridhar Chityala: Okay, the retail chart tells you that relative to the past, two economies or passed two economic or outliers, which is the GFC. We saw in 6 months from March to September the retail sales come back to normalcy. Actually, we can show one more chart which will show later, which is to show the retail sales is slightly about 2019, you know, which is close to about 700 billion dollars of retail sales has occurred during this particular period. So, therefore, the question is, has the targeted impact the targeted stimulus worked in this economy? It did, the numbers show that when you compare this to the past two bubbles, one took almost 34 months another one took 16 months to recover. Now, if you go back to the first chart, which I don’t want you to go back but, think of it you will find the stimulus which was kind of spread over three-four years has delayed the recovery relative to this big induction that occurred. It was pandemic, it was understood to be pandemic and infusion was done.
Sree Iyer: Yes, sir. So, what you are essentially saying is this method that Steve Mnuchin has used has given the country the best chance at having a v-shaped recovery.
Sridhar Chityala: Correct, correct, and the V shape is visible in the chart, you see the way this is why, I use the phrase the United States is an integrated architecture of a balance sheet, which is, you either take a debt to buy an asset or you take a debt to basically incur an expense. So, here the debt was taken which is 2.1 trillion the expense side of the balance sheet showed 4.14 trillion or 4.2trillion for 2020. They added that means these costs were absorbed in the balance sheet as an expense, which means they incurred the expenditure by giving money to people. When you give something away, that means you’re giving money they incurred, that is reflected in the economic outcome because when I look at the revenue side as well, the projection was 3.7 trillion dollars was the revenue which got down to about 3.5 in a major contracted economy, you were able to recover almost 80% or 85-90 % of your taxes, basically because the corporate employment work, the SME employment worked, the payroll taxes, which is a significant part of the revenue worked and individual taxes worked in a pandemic situation with the expenses directly going towards generating the revenue.
Sree Iyer: So for viewers who are trying to grasp all the numbers that SridharJi is putting out. I just want to give you a simplistic example, it’s not the same as what he’s saying, but I want you to understand that many of us have used this handset pumps in India. We use this handset pumps and this is something that draws water from underneath like a boar. Boar has a motor but, in the past 30, 40 or 50 years ago, we used to have this thing called the handset pump and you use a handset pump to pump water from underneath the ground. So, sometimes what would happen if you keep on pumping only air is coming out. So what you have to do is you have to actually pour some water into it to make sure that the air escapes and the pressure builds and then you start pumping and then the water starts coming out. So, it is something like that is what had to be done for covid. So, how much water you put to make sure that the water that is trapped inside comes out that is what has been attempted. I’m sorry to give you a very simplistic example, but that is in essence what the American economy has tried to do and it seems to have done quite well, it’s poised for growth and I think Biden is probably going to harvest some of the fruit of the labour that has done by Trump. But, that doesn’t take away the fact that the common man’s life has largely been, I wouldn’t say undisturbed because covid is hanging over them as like a cloud, but at least in terms of fiscal lifestyle things have been more or less ok, because once this second stimulus comes in, then over a 12-month period people are going to get about five months of their wages assuming they were out of work. Sir, please continue.
Sridhar Chityala: Great. Thank you for that interjection sir. So, these charts are available, by the way, if you go back to three or four sessions ago, you will find the chart that I just mentioned, the numbers are available in that specific chart. So, what’s the next one that you look at? The next one that you look at is the unemployment numbers? So, if you say the numbers are directed towards the corporate and the small business and the public services segments of the economy. What is the unemployment rate? We went from less than 4% unemployment to almost 15% unemployment with close to about 6.9 or 6.7 million people losing jobs, immediately as a result. President Trump at that point of time said, please don’t treat it as people losing jobs, these are not jobs lost is almost consider them as furlough. Furlough simply implies that people are taking a smaller pay cut, they just go, they work the limited time, and they come back in shifts. They may not work until the stimulus came in, once the stimulus came in stimulus the PPP program and the corporate program came in with caveats. It’s not simply given to the business if you take people and we have covered this little bit. If you take people and avail this program, you have to maintain 90% employment either until 2025 or in some instances till 2030.
So, he preserved the employment for all those Industries which availed, all the businesses that availed the program recognizing. And the state’s augmented into two ways, there was also rental assistance that was given in the past, that is also being given in the next stimulus. So, people did not have to either rental or mortgage those who are in, you know concessions were given on the mortgage side, already 100 basis points shift in the interest rates. So, you can see all segments of the economy be it on the expense side of a consumers balance sheet or on the revenue side of a consumers balance sheet, which is effectively income, was managed so that people can assume almost they are living normal lives notwithstanding that they had to deal with this big pandemic situation with no vaccine. He promised that they would be a vaccine by last quarter and vaccine as well has arrived now.
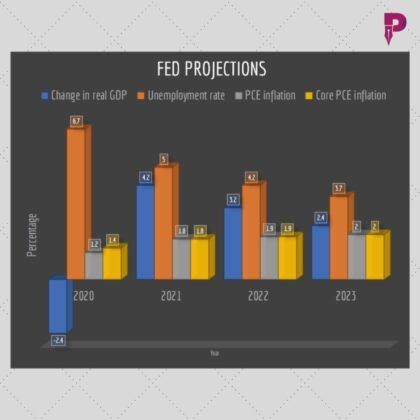
The only question is, you know, whether people would recognize all this was done. By the way, money was given to most of this large Biotech Pharma Companies, 2 billion dollars pre-ordered to Pfizer, something close to a billion dollars to Moderna. They also had given money to European Institution; I don’t remember the name of the institution, Europe and Israel. So, they broadly spread this program of inducing capital into the bioform encouraging them to come up with the vaccines. Okay. Now, why people are not communicating this? They’re not communicating this because there seems to be, I told you, this subjective bias. Even traditional people who are supposed to look at this objectively, are not looking at this objectively. And the last two points that I would like to say is that if there was no pandemic this would be the president who over a period of four years has achieved greater than 3% growth in his entire tenure, relative to 8 years of Obama, which is he never crossed 2% in terms of the GDP growth. So, therefore, that is also the contraction which was expected to be 6% by virtue of this pandemic is now less than 3%, – 2.4% so we actually can go to the next chart. So we talked about the unemployment how we brought the, you see that the chart just like a v-shaped retail sales. It’s an inverted V by what you of inverted v as far as the unemployment is concerned. We went to 14 points, we are now at 6.7%, again within a short span of six months. The unemployment is now roughly around 6.7%. Now if we go to the next chart, which is the, what does the FED say as the economic forecast? We have shared in PGurus the same chart which shows that 2021 looks like a bumper year which the FED says it’s 4.2% growth whereas Goldman Sachs, just two days ago predicted that it expected to be 5%. Now with the stimulus with this incremental dollar value in checks that are going to all the taxpayers who are part of the economy plus there is unemployment plus there is a child allowance etc. There is room to believe that this would be a great year coming into 2021 and still the other question that is asked is why there is no inflation. Inflation occurs when there is a wage rise, here there is no wage rise. The average wage that is given to a person by virtue of this substitution that has occurred is equal to the per capita of the nation. So nobody got, suppose a couple is earning greater than $150,000 they are not entitled to getting this benefit. They would be able to calibrate themselves. So it was meant to address those segments of the economy who paid taxes but who are impacted in a maximum manner. So this is the whole architecture of why you don’t sign find inflation because money was not added as a top of two existing there were no wage increases. So the substitution occurred through the process of stimulus and that in turn helped the unemployment also help the sales, the retail sales to grow, which is the engine of the economy here.
Sree Iyer: Viewers, we just had a bit of a mix-up here. I went back to the right slide, but all the numbers that he mentioned are in the FED projection slide. That’s what we have got it up now. Chityalaji, I have one other slide that I want to show which is the recovery from various market crashes that we’ve had. So shall I go to that now?
Sridhar Chityala: So the other parameter that one needs to look at is the recovery, the markets. The markets and the market sentiments are reflected by the charts, the S&P chart which is how it performed. If you take a look at the S&P chart, looking at any crash that has occurred you find that the one that is the pandemic is the least in terms of the impact and by the way when we look at, that means the peak market down is around 29% relative to the others. Now when you look at the 2020 performance, we are going to be at 15% of 15.6% or 14.7% depending on yesterday, the day before yesterday for 15.6%. Yesterday the market went down. So we will be in that 14.5 to 15% in 2020. We were 29% in 2019. So the markets again have performed quite well under the Trump regime. So this is also another indication that the money is driven by three factors. The three factors are, 1 the interest rates were kept at a manageable level and did not get ahead of, normally the interest rates get ahead of the curve which chokes the consumers in 2 ways, one is the mortgages and the second is the cost of borrowing because everybody is reliant on credit cards or mortgages or auto loans, which basically powers the economy. So interest rates were kept low. Second, inflation was contained, the inflation never went past the target of 2 to 2.5%. So the inflation was kept in check and the third is that there was the support provided by the government to the various sectors of the economy, this is the subsidies battle that went on with China. I agree that in some periods the deficit went up in terms of the trade deficit, but overall when you look at the economic drivers, you will find be it on the inflation side, be it on the interest rate side, be it on unemployment, we achieved the lowest unemployment even going up to 3.5% before we dipped into this pandemic recession that has reflected the market sentiments.
The market sentiments reflect the people’s sentiments, why those charts are important? That chart is important because again when President Trump speaks, look at your 401k balances, which is your retirement account. Look at your 401k balances your 401ks have done very well. If you happen to be a smart guy and put all of your money in the five stars Apple, Alphabet, Facebook Amazon and Google and then also add Tesla. In Tesla, if you invested, in one year you make a significant amount of money. So therefore even in that facet if you find that the performance is quite stellar in by way of his four years of the regime, especially the crisis management around the pandemic.
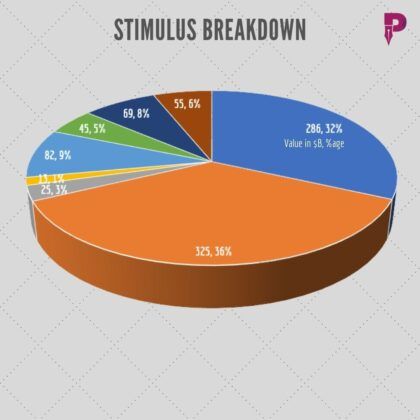
Sree Iyer: And let’s now look at the stimulus break down one more time because this is where things are now back and if you look at this, you will see that there is one spy, which is $55 billion and 6%, it says and this is the weird stuff that nobody has been able to explain and now this was done when the per capita allocation was going to be $600 per person. Now it is going to go from 600 to 2000. Sridharji, you want to take a guess at how this pie chart will change when the government has to accommodate the additional money of $1,400 per person.
Sridhar Chityala: I personally believed that these $ 55 billion dollars, there is a line item which is a little vague as for $27 billion dollars out of the $55 billion within that, you won’t see that number here. But when you see these numbers and apply rounding arithmetic to calculate, so 280 billion dollars for payroll for direct payments, 300 billion dollars for small business PPP Protection Program, $75 billion for rental assistance, $45 million dollars for travel that includes employment or $15 million for travel etc, $82 billion for health services.
So, basically, they’re big line items, they want everybody to be visible, the core segments then suddenly you come to $900 billion, that nobody will tell so we have to add, you remember that we said we were the people to add and basically tell ‘hey, you know, you guys have got this, you know, there’s a problem here.’ The $55 billion is a problem, this awareness prompted the president to kind of stand up and say I don’t like this because this is not something I like. So this $55 billion dollars has to be tackled and you found that money going to a lot of people outside countries, including $1.2 billion to Tibet, $700 million to Sudan and so on. There’s a whole line item of numbers plus there is another line item, which says about $27 billion to some green program or something? It’s very vague you have to search the literature to find out what these numbers are. So these numbers are not very clearly marked, so that’s where he says this is not acceptable. It is US taxpayers money that must go to the US taxpayer in a period of austerity. So I think that’s what we are beginning to see. I mean the question that is asked is what do I see these 55, I just don’t think this is going to be more than 2-3%, it has to come down to something like, less than $10-15 billion. Some of these countries need support especially Tibet because of all the challenges. so Tibet has a very specific focus, it is one of the most oppressed nations which is struggling and the Tibet bill has also been passed and I think we talked about the Tibet Bill. So you will see that they may not unilaterally cut but they’re not going to spend 6% of the budget. They will allocate some chunk of this money towards the incremental Delta.
By the way, just wrap this up, the checks for those direct payments which constitutes $280 billion started to go yesterday, Tuesday, direct payments and checks have started to go yesterday as promised by Steve Mnuchin. So everybody will get their money, yes, there was a lot of cries that a segment of the unemployed people was deprived due to the delay in this budget, maybe by a week or two weeks. They were delayed and but they’re getting the money commencing last night.
Sree Iyer: So let’s take a quick look at the United States elections, by the way, thank you very much for that comprehensive look at the reasons behind the popularity of Donald Trump. See these are all people individuals like you and me who have been asked this question by Gallup and they have responded. So this is directly going to their lifestyle, their bottom line, their feeling of how they feel at the end of the year. So that’s a good analytical view of how this may have come about. So, let’s take a look at the US Elections still the January 6th has a lot of significance, things are happening in Pennsylvania and in Georgia, can you please quickly cover this maybe a minute or so then we can go to India.
Sridhar Chityala: Right. I think the case that the GOP lawmakers in Pennsylvania have come back and said these numbers don’t seem to add up. We’ve now done the analysis on it etc which we have said before that the numbers don’t add up. The Arizona people have stood up and said ‘hey all rests on the shoulders of Mike Pence. We want Pence to intervene and use the separate electoral voters that we ascend rather than the Electoral College because now we find that there is a lot of invalidity in the elections. Georgia also had some interesting issues which is a sitting judge in two counties declined the ruling which prompted the secretary to make a statement. ‘Hey, you know, this is very very illegal. You cannot have, this is people changing their address in the middle of an election process. This is between November 3rd and January 6th and saying that I need to enrol in this new jurisdiction.’ They say that is just not acceptable and that is not the law, but the judge, the word that is used is the Obama judge. She also happens to be the sister of Stacey Abrams who is the Democratic party head saying that the ruling stays and they are allowed and you have accepted. So, therefore, you got some more controversy to come in Georgia. There’s also report that is coming out that basically says that many of the tech companies seem to have played an influential role in Biden selection, again raising concerns. So as far as the elections go all these noises which Democrats would argue is all the noise that you’re making to nullify a genuine election because president-elect Biden got 81 million votes, so it is one of the largest in the history etc.
January 6 appears to be a point of Confrontation where you have had both houses and Republicans raising concerns and they would be raising concerns. All you need is one house and one Republican for a debate to commence and determine how exactly the counting will be done – electoral college or electoral votes which would form the basis for the way forward.
Sree Iyer: Viewers were running a little bit extra time today because there is so much to cover. So now let’s quickly take a look at India for a minute, sir. And then China for a minute and then we can call it a program.
Sridhar Chityala: Yeah. I think that there are three major headlines are India. First is, it looks like India as formally now come out the especially the head of the IAF to basically say China seems to be fully deployed with surface-to-surface missiles, surface-to-air missiles, radar deployment, full-fledged and they also conducted their own kind of practice training in the Canadian Alps to do the winter warfare in the mountains. So it looks they are fairly well organized and orchestrated. So India seems to be cognizant and took a note and was not prepared to withdraw. So they held their positions. They’re now going to have an exercise with the French, the Rafael exercise around the region or around the area. It’s called as the Skyros exercise. It is being held in the Rajasthan region rather than around the border. So they would be doing very similar to the exercises very similar to what Quad went through in the high seas. So that’s the headline on the defence side.
As far as the three specific areas India continues to jump, one is the infrastructure, one of the largest dedicated Freight corridors has been inaugurated by India and that’s 351 kilometres connecting almost to the east. You can see, I think we discussed it again, the entire focus is to actually amplify and elevate the eastern segment of the economy. It has two specific purposes, one is the look-east strategy and two is to develop that region to be a region which broadly covers the Himalayan Kingdom, which is Nepal, Tibet, Bhutan, and Bangladesh, the Eastern segment. So they’re looking at that as a very important block to economically connect them so that you don’t have asymmetric depravation of infrastructure in the region. It’s a great foresight to do that and freight basically because that is goods moving, goods coming encourages trade and also the commercial movement that can go along with it. The other area is UP, with Maharashtra having some political kind of conflicts and issues between the centre and the entire infrastructure seems to be working around at least three to four states. One is UP which is getting a huge amount of infrastructure left, now, they are building their roadways, which is one of the largest roadway network connections, with Purvanchal Highway and the Bundelkhand and the Gorakhpur which are all interconnected as highways, creating something close to about 600-700-800 kilometres of national highways. So there seems to be a very clear focus to build the GDP of Uttar Pradesh, the Uttar Pradesh GDP is around $250 billion. Clearly, the goal is they have a master plan to build that as a one trillion economy. Similarly. I think the other states like Rajasthan, MP, Gujarat, you see a lot of infrastructure besides the northeastern side.
The third reform which is taking place is around the mining sector, so the mining sector was one of the big sectors which were announced in the stimulus bill, which is the dilution so that you can bring, so this is the balance sheet model, asset, liability, income, and expenses. So how do you find the expenses to create the stimulus? You need to create something on the asset side, so you are selling the assets rather than borrowing, you are borrowing but you’re also kind of selling some of the assets to fund. So you have that reform going simultaneously as well.
Everybody knows India is ready for covid and moving forward. So these are some of the positives which are interesting. This is where all the visits are – security, infrastructure, and trade is the pivotal format both domestically, as well as globally. what India is trying to pursue as an integrated policy.
Sree Iyer: Last one, sir, on China. All the developments that are happening on China, the United States has roundly condemned the arrest of the citizen journalists from Hong Kong and one of the lawmakers is now being detained. And China is again beginning to rattle sabres. What do you make of it, sir? And the last one is the status of the ships that are still waiting to Dock and that Dalian has still not happened. So kindly, summarize it for us before we wrap up this program.
Sridhar Chityala: We will start with Dalian yard because there’s quite a bit of Indian national staff or crude dark, the stalemate continues. They have been sitting there for more than six months.
I won’t say they are impacted because they’re not able to some crucial crew changes, but they’re getting medical supplies and anything that they need to do, but they’re all docked for six months in a boat. So that impasse continues. India has reciprocated with an equally good gesture which is to say no Chinese National can board an Indian Airplane or an Airplane, which they use to go via Europe and come into India, so they basically have said, ‘thank you. No, thank you, and we don’t need you here if you don’t want to treat our citizens’
Hong Kong, the journalist as you rightly said has been unilaterally condemned. The United States has imposed more sanctions now on companies, company’s subsidiaries, any company dealing with the Chinese PLA.
Well, Japan has now joined a partnership with the other RCEP members and said they’re going to push if they want to be part of RCEP as they want to, then there should be free, data-free flows and data-free access available to all and they have to follow certain rules. China is not a country which follows rules. so it’ll be interesting to see what happens to that specific confrontation.
Then, the Chinese delegation went to Nepal to meet Mr Oli because the Communist Party appears to be splitting and there seem to be the people who are very candid about it, people who are unified so that they are agenda, the Communist agenda can be propagated. That seems to have fallen and backfired and Oli has refused to meet the delegation. And at least we are all grateful that they have not fallen into the trap and not impacted the sovereignty. Otherwise, Nepal would have gone very similar to the Tibetan model which one day would be absorbed into as another province in China. So I think you can see across the globe China seems to have problems, the United States, India which we touched on, Nepal which we touched on, Asia, in Japan, Hong Kong, of course, we talked yesterday when we presented the maps around Taiwan.
Sree Iyer: Thank you, sir. And viewers do subscribe to our Channel. And please also like our video, this helps us in increasing our subscription more because then it gets shown to more people that are visiting YouTube. So please help us in this cause we want to hit the 1 million mark as soon as possible. Sridharji, thank you very much for devoting precious time of yours in coming up with all these data. I hope viewers found it useful. And once again, thank you very much. And we’ll see you tomorrow with more news on what is happening on Nashville what is happening in and around the United States, a lot of stuff to discuss. But today we don’t have time for that and plus things are still in a state of flux.
Namaskar and thank you very much.
Sridhar Chityala: Namaskar and have a wonderful day. Thank you
- Rahul Hood read the Right story (Robin Hood) but applied it to the wrong oppressed - April 24, 2024
- Xi Jinping treats Chinese people like Ganna (Sugarcane) – Squeeze them & throw them away! - April 9, 2024
- Tharoor Aadat se Majboor - April 7, 2024